Introduction
Les algorithmes utilisés par les intelligences artificielles génératives comme ChatGPT sont basés sur des réseaux de neurones profonds, donc sur des notions mathématiques avancées et beaucoup d'algorithmique. Ils sont trop complexes pour être présentés ici.
En revanche, l'algorithme que nous allons aborder dans cette seconde partie d'énigme est beaucoup plus simple à comprendre et se classe parmi les algorithmes d'intelligence artificielle, c'est en quelle sorte "le plus simple" des algorithmes d'IA !
Algorithme des $k$ plus proches voisins
L’algorithme des k plus proches voisins appartient à la famille des algorithmes d'apprentissage automatique (machine learning) qui constituent le poumon de l'intelligence artificielle actuellement. Plus précisément, il s'agit d'un algorithme permettant de résoudre un problème de classification.
Pour simplifier, l'apprentissage automatique part souvent de données connues et essaie de dire quelque chose des données qui n'ont pas encore été vues : son but est de généraliser, de prédire.
Cet algorithme est souvent abrégé kppv. En anglais, on dit k nearest neighbors souvent abrégé knn.
Magré sa simplicité, l'algorithme des $k$ plus proches voisins a été utilisé dans de nombreux domaines :
- des systèmes de recommandations automatiques aux utilisateurs sur le Web,
- dans la finance : pour aider les banques à évaluer le risque d'un prêt à un individu ou à une entreprise, mais aussi pour des prédictions boursières, des analyses de blanchiment d'argent, etc.,
- dans la santé : pour faire des prédictions sur le risque de crises cardiaques et de cancer de la prostate,
- dans la reconnaissance de caractères : pour identifier des numéros manuscrits, par exemple sur des formulaires ou des enveloppes postales.
Présentation de l'algorithme des kppv

On dispose de données sur 34 Pokémons : leur type (Psy ou Eau), leur points de vie et la valeur de leurs attaques. On peut représenter ces données graphiquement, avec les valeurs d'attaque en abscisses et les points de vie en ordonnées.
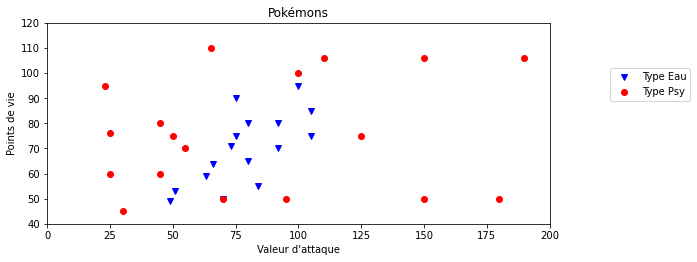
Les Pokémons de type "Eau" sont représentés pas les points bleus, et ceux de type "Psy" par les points rouges.
Problème : Peut-on prédire le type d'un nouveau Pokemon inconnu ?

Ce problème, qui demande à prédire à quelle catégorie, ou classe, appartient ce nouvel élément donné, est appelé problème de classification. L'algorithme des $k$ plus proches voisins permet de trouver les $k$ voisins les plus proches (si $k$ = 5 on cherche les 5 voisins les plus proches) de ce nouvel élément dans le but de lui associer une classe plausible (Psy ou Eau, dans cet exemple) qui sera la classe majoritaire (la plus présente) parmi les $k$ plus proches voisins.
Voyons quelques exemples avec différentes valeurs de $k$ avant de passer à l'énigme.
Influence de la valeur de $k$
La valeur de $k$ est très importante, elle doit être choisie judicieusement car elle a une influence forte sur la prédiction. Regardons le résultat de la prédiction pour différentes valeurs de $k$ sur notre exemple.
Exemple 1 : le 1 plus proche voisin ($k=1$)
Si $k = 1$, cela revient à chercher la donnée la plus proche de notre élément cible. Ici, on se rend compte que sa classe est "Psy" (point rouge) donc on classerait le nouveau Pokémon comme étant de type "Psy".

Exemple 2 : les 5 plus proches voisins ($k=5$)
On se rend compte que la classe majoritaire dans les 5 plus proches voisins est "Psy" (3 points rouges contre 2 points bleus) donc on classerait le Pokemon inconnu comme étant de type "Psy".

Exemple 3 : les 9 plus proches voisins ($k=9$)
On se rend compte que la classe majoritaire dans les 9 plus proches voisins est "Eau" (5 points bleus contre 4 points rouges) donc on classerait le Pokemon inconnu comme étant de type "Eau".

En poursuivant, si on choisit $k=34$ (le nombre total de données), alors la prédiction serait toujours "Psy" car c'est la classe majoritaire de l'échantillon (il y a 18 "Psy" et 16 "Eau"). Il est donc incorrect de penser que plus la valeur de $k$ augmente meilleure sera la prédiction, c'est plus complexe que cela (voir le paragraphe après l'énigme si vous le souhaitez).
Calcul de la distance entre deux points
L'algorithme des $k$ plus proches voisins repose presque entièrement sur la distance entre deux données. Dans les exemples vus précédemment, c'est la distance "naturelle" qui a été choisie (celle "à vol d'oiseau"), on parle de distance euclidienne.
Elle se calcule avec la formule vue en classe de Seconde en cours de mathématiques, que l'on rappelle : dans un repère orthonormé, si $A$ et $B$ ont pour coordonnées respectives $(x_A, y_A)$ et $(x_B, y_B)$ alors la distance entre ces deux points est donnée par la formule :
$$\text{distance}(A, B) = \sqrt{(x_B-x_A)^2 + (y_B-y_A)^2}.$$
Exemples
On donne des points dans un repère orthonormé. Chaque point possède une classe : Rouge ou Bleue. On va appliquer l'algorithme des $k$ plus proches voisins pour prédire la classe (Rouge ou Bleue) de plusieurs nouveaux points pour différentes valeurs de $k$.
On utilise la distance euclidienne (naturelle) pour l'algorithme des $k$ plus proches voisins.

Cas n°1 : Prédiction de la classe du point $M(1; 3)$ avec $k=3$
C'est un cas "facile", au sens où l'on peut trouver graphiquement les 3 points les plus proches de $M(1; 3)$ (sans calculer les distances) : il s'agit des points $D$, $B$ et $A$.
Parmi ces trois points, la classe Bleue est majoritaire (2 contre 1) donc on prédit que $M$ est de classe Bleue.
Cas n°2 : Prédiction de la classe du point $N(3,5; 4)$ avec $k=5$
On commence par calculer la distance entre le point $N$ et tous les autres, en utilisant la formule rappelée plus haut (on ne détaille les calculs que pour les 3 premiers points) :
- $\text{distance}(A, N) = \sqrt{(x_N-x_A)^2 + (y_N-y_A)^2} = \sqrt{(3.5-1)^2 + (4-1)^2} \simeq 3.905$
- $\text{distance}(B, N) = \sqrt{(x_N-x_B)^2 + (y_N-y_B)^2} = \sqrt{(3.5-2)^2 + (4-2)^2} = 2.5$
- $\text{distance}(C, N) = \sqrt{(x_N-x_C)^2 + (y_N-y_C)^2} = \sqrt{(3.5-4)^2 + (4-2)^2} \simeq 2.062$
- $\text{distance}(D, N) \simeq 1.803$
- $\text{distance}(E, N) \simeq 1.118$
- $\text{distance}(F, N) \simeq 1.118$
- $\text{distance}(G, N) \simeq 1.803$
- $\text{distance}(H, N) = 2.5$
- $\text{distance}(I, N) \simeq 1.803$
Les 5 points les plus proches de $N$ sont donc, dans l'ordre : $E$ (Bleue), $F$ (Rouge), $D$ (Rouge), $G$ (Rouge) et $I$ (Rouge). Parmi ces 5 points, la classe Rouge est majoritaire (4 contre 1) donc on prédit que $N$ est de classe Rouge.
👁️ Pour aller plus loin ...
Quelle valeur de $k$ faut-il choisir ?
La valeur de $k$ a une importance fondamentale, car la prédiction n'est pas la même selon la valeur choisie. Quelle valeur faut-il choisir ?
Pour trouver une bonne valeur de $k$, il est possible d'appliquer le protocole expérimental suivant avec différentes valeurs de $k$ et regarder celle qui donne les meilleurs résultats :
- Séparer les données connues (!) en deux paquets : un paquet pour entraîner le modèle (90 % par exemple), un second pour tester le modèle (les 10% restants)
- Utiliser le premier paquet comme nouveau jeu de données et appliquer l'algorithme des kppv sur les éléments qui ont été retirés
- Comparer les réponses de l'algorithme avec les réponses attendues (on connaît la classe des éléments retirés donc on peut comparer)
Il est même judicieux de recommencer le protocole en retirant d'autres données pour affiner encore davantage la recherche de la meilleure valeur $k$ : on parle alors de validation croisée qui est une méthode d'apprentissage.
Choix de la distance
On a utilisé la distance euclidienne dans nos exemples, mais sachez qu'il est possible de choisir d'autres distances, plus pertinentes selon la situation et la répartition des points.
Par exemple, on peut très bien imaginer que les valeurs sur l'axe des ordonnées ne nous intéressent pas et utiliser une distance ne prenant en compte que l'axe des abscisses avec la formule $\text{distance}(A, B) = |x_B-x_A|$ (c'est-à-dire la valeur absolue de $x_B-x_A$). Ainsi, sur notre exemple, et avec cette distance, la classe majoritaire des 9 plus proches voisins de notre nouveau Pokémon est "Psy" (6 points rouges contre 3 points bleus), ce qui donnerait une prédiction contraire à celle donnée en utilisant la distance "naturelle" (euclidienne) :

On voit donc que le choix de la distance n'est pas anodin et que ce choix peut aboutir à des prédictions différentes.
Un algorithme d'intelligence artificielle ? Vraiment ?
L'algorithme des $k$ plus proches voisins permet de prédire la classe d'une donnée inconnue, c'est en cela qu'on peut le considérer comme un algorithme intelligent. Il fait partie de la catégorie des algorithmes d'apprentissage automatique (une branche de l'IA) mais il s'agit plus d'un apprentissage par coeur : il doit utiliser toutes les données qu'il connait pour effectuer les calculs (de distance) pour chaque prédiction, et si on lui enlève ce jeu de données de départ, il ne peut plus rien prédire.
La plupart des autres algorithmes d'apprentissage automatique, ont une forme d'intelligence plus poussée : ils cherchent à apprendre quelque chose du jeu de données qui leur est fourni, c'est-à-dire à remplacer les données par un modèle (une sorte de "règle" permettant de classer les données, de prendre une décision, etc.). Autrement dit, un tel algorithme tente de "comprendre" les données pour en déduire un modèle.
Pour illustrer cela de manière simplifiée, un algorithme d'apprentissage automatique basé sur un réseau de neurones artificiels chercherait par exemple, à partir des données, à délimiter deux "zones" séparant les Pokémons "Psy" des Pokémons "Eau" :

Il n'aurait alors plus besoin des données (des points) pour prédire la classe d'un nouvel élément car il suffirait de regarder dans quelle zone celui-ci se trouve (d'utiliser le modèle qu'il a deviné).
🔎 Énigme 🔎
On considère pour cette énigme un jeu de données sur deux espèces d'iris : versicolor et virginica.

Iris versicolor

Iris virginica
Plus précisément, on possède des données connues sur la longueur et la largeur de différents pétales ainsi que leur espèce (qui est donc ici la classe de l'iris). Voici ces données :
| Longueur pétale (en cm) | Largeur pétale (en cm) | Espèce |
|---|---|---|
| 4.5 | 1.5 | versicolor |
| 4.5 | 1.5 | versicolor |
| 4.8 | 1.8 | versicolor |
| 4.9 | 1.5 | versicolor |
| 5 | 1.7 | versicolor |
| 4.5 | 1.7 | versicolor |
| 5.1 | 1.6 | versicolor |
| 5.25 | 1.7 | versicolor |
| 5.1 | 2 | virginica |
| 5.3 | 1.9 | virginica |
| 5 | 2 | virginica |
| 5.5 | 1.8 | virginica |
| 5 | 1.5 | virginica |
| 4.9 | 2 | virginica |
| 5 | 1.8 | virginica |
En réalité, le jeu de données est plus complet, mais pour que les calculs restent en nombre raisonnable on se limite aux données ci-dessus.
On peut représenter ces données graphiquement :
On voit apparaître deux "zones" quasiment distinctes entre les deux espèces, ce qui permettra de faire des prédictions assez fiables à l'aide de l'algorithme des $k$ plus proches voisins.
On considère un pétale d'iris inconnu, ayant une longueur et une largeur respectivement égales à $5,1$ cm et $1,8$ cm. On veut prédire sa classe : 1 pour versicolor et 2 pour virginica.
La réponse à cette seconde partie de l'énigme est composée des réponses aux trois questions suivantes.
- Quelle est la classe de ce pétale si on applique l'algorithme des $k$ plus proches voisins avec la valeur $k=3$ ?
- Quelle est la classe de ce pétale si on applique l'algorithme des $k$ plus proches voisins avec la valeur $k=5$ ?
- Quelle est la classe de ce pétale si on applique l'algorithme des $k$ plus proches voisins avec la valeur $k=7$ ?
Attention, la réponse est à donner en supprimant les espaces entre les trois réponses. Par exemple, si les prédictions sont dans l'ordre versicolor, virginica puis versicolor, la réponse attendue est 121.
Aide : pour ne pas avoir besoin de faire les calculs à la main ou à la calculatrice, vous pouvez utiliser la page suivante :
Selon les calculs, l'ordinateur peut donner des résultats "approchés", ne vous en préoccupez pas. (Ce ne sont pas des erreurs de l'ordinateur, il ne peut tout simplement parfois pas faire mieux... on explique cela en spécialité NSI en Première).
