Introduction

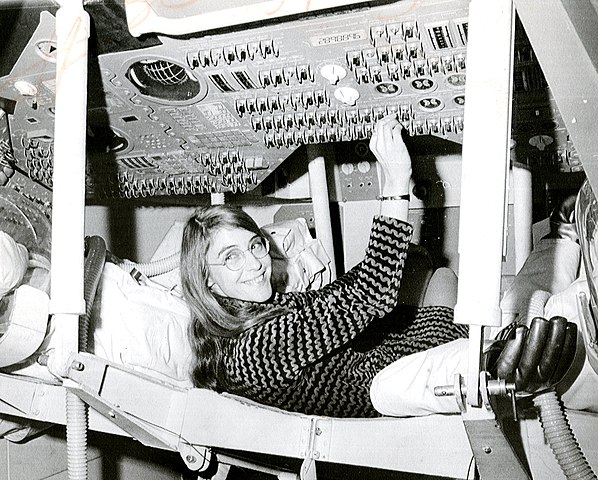
Margaret Hamilton a conçu, au sein du MIT, le système embarqué du programme spatial Apollo, c'est-à-dire l'ensemble des logiciels ayant permis au vaisseau spatial de se poser sur la Lune, et à l'Homme d'y poser le pied le 21 juillet 1969.

Voici une vidéo sur Margaret Hamilton retraçant rapidement son histoire et son travail au sein de la mission Apollo.

Margaret Hamilton

Les logiciels qu'elle a développés pour la mission Apollo, ont permis de poser les bases de l'informatique moderne, notamment la priorisation des tâches utilisée actuellement par tous nos ordinateurs, smartphones, télévisions, etc.

La suite de l'énigme ci-dessous propose d'expliquer comment un ordinateur peut exécuter plusieurs tâches simultanément et on terminera par la manière dont un ordinateur peut donner la priorité à certaines tâches, ce qui a été la grande idée novatrice apportée par Margaret Hamilton pour le projet Apollo (et qui a sauvé la vie aux astronautes).

Deuxième partie de l'énigme

Introduction

Pour vous cela semble normal de pouvoir ouvrir simultanément un navigateur Web, un traitement de texte, un logiciel pour écouter de la musique... En effet, les systèmes d'exploitation actuels (Linux, macOS, iOS, Android, Windows…) permettent d’exécuter des programmes “simultanément”. Mais ce n'était pas le cas des ordinateurs personnels de l'époque !

Dans les années 1960-1970 les premiers ordinateurs personnels étaient incapables d’exécuter plusieurs programmes à la fois : il fallait attendre qu’un programme lancé se termine pour en exécuter un autre (il fallait fermer le traitement de texte pour pouvoir lancer le logiciel de musique, en admettant que de tels programmes existaient à l'époque !).

Nous allons désormais voir les idées permettant à plusieurs programmes d'être exécutés simultanément, comme le font les ordinateurs actuels. Une énigme est posée à la fin pour valider votre compréhension !

On expliquera après l'énigme comment attribuer des priorités à certains programmes, comme l'a fait Margaret Hamilton !

Une instruction à la fois

Concrètement, un programme informatique est une suite de plusieurs instructions élémentaires (c'est-à-dire de plusieurs séries de "0" et de "1") qui doivent être exécutées par le processeur d'un ordinateur. Ce dernier ne peut exécuter qu'une seule instruction à la fois (qu'il s'agisse d'un ordinateur ancien ou récent).

Pour simplifier, on considérera qu'il faut une unité de temps pour exécuter une instruction élémentaire.

Ainsi, si un programme R se décompose en dix instructions élémentaires, il faudra 10 unités de temps pour l'exécuter. On peut alors représenter ce programme de la façon suivante 🟥🟥🟥🟥🟥🟥🟥🟥🟥🟥, où chaque carré représente une instruction élémentaire.

Dans toute la suite, on considérera trois programmes R, B et N qui doivent être exécutés par un ordinateur :

Les premiers ordinateurs : des programmes exécutés l'un après l'autre

Dans les années 1970 les ordinateurs personnels étaient incapables d’exécuter plusieurs tâches à la fois : il fallait attendre qu’un programme lancé se termine pour en exécuter un autre.

Dans ce cas, les programmes s'exécutent (entièrement) dans l'ordre où ils arrivent. Par exemple, si les trois programmes R, B et N arrivent dans cet ordre à l'instant $t=0$ (B arrive juste après R, et N arrive juste après B), alors leur exécution se fait de la façon suivante :

🟥🟥🟥🟥🟥🟥🟥🟥🟥🟥🟦🟦🟦🟦🟦⬛⬛⬛

Chaque programme n'est exécuté que lorsque le précédent est terminé.

Alternance entre les programmes

À la même époque, le système développé par Margaret Hamilton pouvait gérer l'exécution de plusieurs programmes en même temps.

Comment un processeur, qui ne peut exécuter qu'une seule instruction à la fois, arrive-t-il à donner l'impression que tous les programmes sont exécutés simultanément ?

C'est possible car un programme est une suite des plusieurs instructions. Il est donc possible d'exécuter les premières instructions d'un programme (par exemple 🟥🟥🟥) puis le mettre "en pause" pour exécuter quelques instructions d'un autre programme (par exemple 🟦🟦), ainsi de suite jusqu'à revenir au premier programme qui peut alors se poursuivre, puis le second, etc.

Évidemment, cela semble simple en théorie mais en pratique, il fallait réussir à mettre en oeuvre des mécanismes permettant de pouvoir stopper un programme, en exécuter un autre, tout en mémorisant où le premier s'est arrêté afin de reprendre son exécution au bon endroit lorsque c'est à nouveau son tour.

Comme un ordinateur actuel peut exécuter des millions d'instructions par seconde, cela donne l'impression d'une exécution simultanée, alors qu'en réalité les programmes sont exécutés par "petits morceaux" à tour de rôle, de manière si rapide que l'on ne s'en rend par compte.

Choix de l'ordre d'exécution

Pour que plusieurs programmes puissent être exécutés "simultanément", une façon simple de procéder est d'appliquer la politique du tourniquet : les différents programmes se partagent le temps d'exécution à tour de rôle.

Concrètement, une tranche de temps est définie (ce sera 4 unités de temps par la suite), et chaque programme n'est exécuté que pendant cette tranche de temps, puis c'est au suivant et ainsi de suite, jusqu'à revenir au premier programme qui peut reprendre le cours de son exécution, etc.

Dans toute la suite, on supposera que la tranche de temps, appelée aussi quantum, est égale à 4 unités de temps.

Exemple 1 : Un cas simple

Par exemple, si les programmes R, B et N précédents (arrivés dans cet ordre au même moment) s'exécutent par tranche de 4 unités de temps avant de passer la main au suivant, alors leur exécution se fait de la façon suivante :

🟥🟥🟥🟥🟦🟦🟦🟦⬛⬛⬛🟥🟥🟥🟥🟦🟥🟥

R s'exécute pendant la tranche de temps (ses 4 premières instructions sont exécutées), puis c'est B, puis c'est N. Comme N est terminé avant la tranche de temps définie, c'est R qui reprend directement, etc.

Chaque programme est ainsi exécuté petit à petit grâce à une rotation (le tout très rapidement bien sûr, on a l'impression qu'ils sont exécutés simultanément).

Exemple 2 : Et si les programmes n'arrivent pas au même moment ?

Il n'est pas rare que des programmes doivent être exécutés alors que d'autres sont déjà en cours d'exécution (par exemple, si on lance un navigateur Web alors qu'on est déjà en train d'écouter de la musique et de rédiger un document avec un traitement de texte).

Si les programmes n'arrivent pas au même moment pour être exécutés, il suffit de les inclure dans la rotation à partir du moment où ils arrivent. Pour cela on va utiliser ce qu'on appelle une file d'attente.

On notera "< <" la file d'attente, le sens des flèches indiquant le sens de la file, où le premier programme à entrer dans la file sera le premier à en sortir. Exemples :

L'algorithme est assez simple et suit les trois idées suivantes :

Par exemple, on reprend nos trois programmes R, B et N mais cette fois-ci ils arrivent à des moments différents :

Le tableau ci-dessous montre chronologiquement l'état de la file et dans quel ordre les programmes vont s'exécuter :

temps R(10) B(5) N(3) File d'attente Explication
0 🟥 < < file d'attente vide
1 🟥
2 🟥 < B < $t=2$ : B est placé en file d'attente
3 🟥
4 🟦 < R < $t=4$ : B est élu, R est placé en file d'attente
5 🟦 < R, N < $t=5$ : N est placé en file d'attente
6 🟦
7 🟦
8 🟥 < N, B < $t=8$ : R est élu, B est placé en file d'attente
9 🟥
10 🟥
11 🟥
12 ⬛ < B, R < $t=12$ : N est élu, R est placé en file d'attente
13 ⬛
14 ⬛
15 🟦 < R < $t=15$ : B est élu, (N est terminé)
16 🟥 < < $t=16$ : R est élu, file d'attente vide
17 🟥

En particulier, on voit que :

Bilan : Dans notre cas, leur exécution se fait de la façon suivante :

🟥🟥🟥🟥🟦🟦🟦🟦🟥🟥🟥🟥⬛⬛⬛🟦🟥🟥

Exemple 3 : Un dernier avant l'énigme

Avant de passer à l'énigme, un dernier exemple pour la route !

Il y a toujours nos trois programmes R, B et N qui doivent être exécutés, mais leurs moments d'arrivée sont encore différents :

temps R(10) B(5) N(3) File d'attente Explication
0 🟥 < < file d'attente vide
1 🟥
2 🟥 < B < $t=2$ : B est placé en file d'attente
3 🟥 < B, N < $t=3$ : N est placé en file d'attente
4 🟦 < N, R < $t=4$ : B est élu, R est placé en file d'attente
5 🟦
6 🟦
7 🟦
8 ⬛ < R, B < $t=8$ : N est élu, B est placé en file d'attente
9 ⬛
10 ⬛
11 🟥 < B < $t=11$ : R est élu, N est terminé
12 🟥
13 🟥
14 🟥
15 🟦 < R < $t=15$ : B est élu, R est placé en file d'attente
16 🟥 < < $t=16$ : R est élu, B est terminé, file d'attente vide
17 🟥

Donc les 3 programmes s'exécutent dans l'ordre suivant :

🟥🟥🟥🟥🟦🟦🟦🟦⬛⬛⬛🟥🟥🟥🟥🟦🟥🟥

👁️ Pour aller plus loin : ajout de priorités aux programmes

On vient de voir comment un ordinateur peut exécuter plusieurs programmes "simultanément" sans qu'il faille attendre que l'un soit terminé pour en exécuter un autre.

L'ordinateur du module Apollo permettait cette exécution simultanée, alors que ce n'était pas le cas pour les ordinateurs personnels de l'époque. Mais comme dit en introduction, le système développé par Margaret Hamilton et son équipe permettait également d'attribuer des priorités aux différents programmes, de telle manière que les tâches ayant la plus haute priorité puissent interrompre des tâches moins prioritaires. Ainsi, le programme destiné à l'atterrissage (prioritaire) a pu interrompre les autres programmes en cours (moins prioritaires) juste avant l'arrivée sur la Lune, afin que toutes les ressources de calculs de l'ordinateur soient utilisées pour poser la navette sur la Lune.

C'est grâce à cela que le module lunaire Apollo a pu se poser sur la Lune puisque le programme destiné à l'atterrissage a pu interrompre les autres programmes en cours juste avant l'arrivée sur la Lune, afin que toutes les ressources de calculs de l'ordinateur soient consacrées à la phase d'alunissage.

Le principe de priorités

À chaque programme est associé un niveau de priorité, par exemple 1 et 2, la priorité 2 étant plus prioritaire que 1.

Pour permettre à un programme plus prioritaire d'être exécuté avant d'autres moins prioritaires arrivés avant lui, il y a deux idées, finalement assez simples :

Exemple

On reprend nos programmes de l'exemple 2 mais qui ont cette fois des priorités différentes :

La différence avec l'ordre d'exécution de l'exemple 2 se verra à l'instant $t=8$ puisque R et N seront en attente mais ce sera N qui sera élu car sa priorité est plus élevée (bien qu'il soit placé après R dans les files d'attente) :

temps R(10) B(5) N(3) Files d'attente Explication
0 🟥 priorité 2 : < <
priorité 1 : < <		 files d'attentes vides
1 🟥
2 🟥 priorité 2 : < <
priorité 1 : < B <		 $t=2$ : B arrive
3 🟥
4 🟦 priorité 2 : < <
priorité 1 : < R <		 $t=4$ : B est élu
5 🟦 priorité 2 : < N <
priorité 1 : < R <		 $t=5$ : N arrive
6 🟦
7 🟦
8 ⬛ priorité 2 : < <
priorité 1 : < R, B <		 $t=8$ : **N est élu**
car prioritaire devant R
9 ⬛
10 ⬛
11 🟥 priorité 2 : < <
priorité 1 : < B <
12 🟥
13 🟥
14 🟥
15 🟦 priorité 2 : < <
priorité 1 : < R <		 $t=15$ : B est élu
16 🟥 priorité 2 : < <
priorité 1 : < <		 $t=16$ : R est élu
17 🟥

Par analogie avec le programme Apollo, on peut considérer que le programme N est celui permettant de poser le module sur la Lune, qui a été exécuté avant les autres moins prioritaires : cela a permis à l'ordinateur de bord de consacrer toute sa mémoire à cette tâche, ce qui a sauvé la vie des astronautes car la mémoire de l'ordinateur était alors saturée par d'autres informations (il y avait beaucoup de programmes en file d'attente et s'il n'y avait eu qu'une seule file d'attente, N aurait attendu trop longtemps avant d'être exécuté et le module se serait probablement écrasé sur la Lune).

En réalité, les systèmes d'exploitation actuels (de vos ordinateurs, smartphones, etc.) gèrent plusieurs centaines ou milliers de programmes simultanément, et utilisent bien plus que deux niveaux de priorité (par exemple sous Linux, les priorités vont de -20 à 20), le niveau de priorité d'un programme pouvant changer dynamiquement au cours du temps afin d'éviter que certains programmes ne monopolisent toutes les ressources pendant trop longtemps.

🔎 Énigme 🔎

Pour cette seconde partie de l'énigme, on considère les quatre programmes suivants :

Déterminez l'ordre d'exécution de ces quatre programmes